Бейсбол – один из самых математических видов спорта, в котором все, начиная от подачи и заканчивая ударом, подчиняется числам и статистике. Именно с него началось внедрение статистики в другие виды спорта. Математика для исследования бейсбола применяется как глубокий анализ бейсбольной статистики для максимально объективного понимания игры. Этот анализ - саберметрика, и многие профессиональные бетторы применяют ее для разработки собственной системы ставок на бейсбол.
Саберметрика в бейсболе
Самый большой сторонник данного метода, Билл Джеймс, вывел формулу, которая может определить приближенное значение процента бейсбольных матчей, выигранных командой:
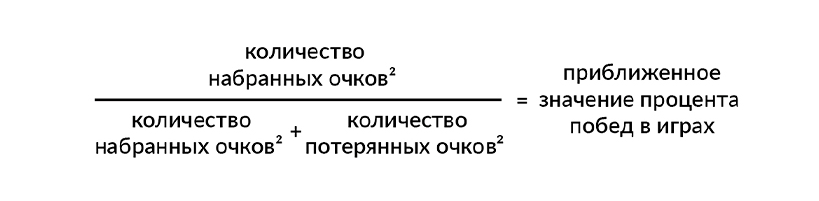
Процент побед, который возможно спрогнозировать с помощью данной формулы, находится между 0 и 1, как и любая другая вероятность. Это число возрастает как с увеличением количества очков, набранных в играх, так и с уменьшением количества потерянных в играх очков.
Теорема Пифагора – основа для игроков, делающих ставки на бейсбол
Эту формулу Билл Джеймс назвал “бейсбольной теоремой Пифагора”. Дело в том, что оригинальная теорема Пифагора утверждает, что треугольник является прямоугольным только тогда, когда сумма квадратов двух его сторон равна сумме квадрата гипотенузы. Именно из-за суммирования в теореме Пифагора двух квадратов чисел Билл Джеймс выбрал такое название для своей формулы.
Как применять эту формулу?
R = количество набранных очков/количество потерянных очков.
R2 / R 2 + 1 = приближенное значение процента побед в играх.
Для примеров мы будем использовать данные для каждой серии игр МЛБ с выбыванием (1980 – 2007). В 2006 году Detroit Tigers набрали 822 очка, а потеряли 675. Следовательно, показатель набора очков Detroit Tigers в 2006 году составил R = 822 / 675 = 1,218. Исходя из теоремы Пифагора, прогнозируемый процент побед Detroit Tigers равен 1,2182 / (1,218)2 + 1 = 0,597.
Как сложился 2006 год для Detroit Tigers в реальности? В регулярном сезоне команда выиграла 95 игр из 162, их процент равен 95 / 162 = 0,586. Поскольку ожидаемый процент побед равен 0,597, а в действительности он составил 0,586, погрешность данной формулы для прогнозирования процента игр, в которых Detroit Tigers победила в сезоне 2006, равна 1,1%.
Как рассчитать погрешность прогнозирования для ставок на бейсбол?
Погрешность при прогнозировании процента побед для каждой команды рассчитывается как реальный процент побед минус прогнозируемый. Она бывает как положительной, так и отрицательной:
- Положительная погрешность прогнозируемого процента побед – команда выиграла больше игр, чем прогнозировалось. Для Boston Red Sox в 2006 году она составила 0,531 - 0,497 = 0,034.
- Отрицательная погрешность – команда выиграла меньше игр, чем спрогнозировано. Погрешность для Arizona Diamondbacks в 2006 году составила 0,469 − 0,490 = -0,021.
В таблице ниже приведены расчеты, полученные при использовании теоремы:
- A - команда
- B - количество побед/поражений
- C - количество набранных/потерянных очков
- D - показатель набора очков
- E - прогнозируемый процент побед
- F - реальный процент побед
- G - абсолютная погрешность
| A | B | C | D | E | F | G | ||
| Diamond | 76/86 | 773/788 | 0,981 | 0,490 | 0,469 | 0,021 | ||
| Braves | 79/83 | 849/805 | 1,055 | 0,527 | 0,488 | 0,039 | ||
| Orioles | 70/92 | 768/899 | 0,854 | 0,422 | 0,432 | 0,010 | ||
| Red Sox | 86/76 | 820/825 | 0,994 | 0,497 | 0,531 | 0,034 | ||
| White Sox | 90/72 | 868/794 | 1,093 | 0,544 | 0,556 | 0,011 | ||
| Cubs | 66/96 | 716/834 | 0,859 | 0,424 | 0,407 | 0,017 | ||
| Reds | 80/82 | 749/801 | 0,935 | 0,466 | 0,494 | 0,027 | ||
| Indians | 78/84 | 870/782 | 1,113 | 0,553 | 0,481 | 0,072 | ||
| Rockies | 76/86 | 813/812 | 1,001 | 0,501 | 0,469 | 0,031 | ||
| Tigers | 95/67 | 822/675 | 1,218 | 0,597 | 0,586 | 0,011 | ||
| Marlins | 78/84 | 758/772 | 0,982 | 0,491 | 0,481 | 0,009 | ||
| Astros | 82/80 | 735/719 | 1,022 | 0,511 | 0,506 | 0,005 | ||
| Royals | 62/100 | 757/971 | 0,780 | 0,378 | 0,383 | 0,005 | ||
| Angels | 89/73 | 766/732 | 1,046 | 0,523 | 0,549 | 0,027 | ||
| Dodgers | 88/74 | 820/751 | 1,092 | 0,544 | 0,543 | 0,001 | ||
| Brewers | 75/87 | 730/833 | 0,876 | 0,434 | 0,463 | 0,029 | ||
| Twins | 96/66 | 801/683 | 1,173 | 0,579 | 0,593 | 0,014 | ||
| Yankees | 97/65 | 930/767 | 1,213 | 0,595 | 0,599 | 0,004 | ||
Здесь особое внимание стоит обратить на колонку G, где указано абсолютное значение погрешности для каждой команды (то есть, без учета положительного или отрицательного значения). Для того, чтобы понять, насколько правильно прогнозируемый процент команды побед аппроксимирует реальный процент, абсолютные показатели погрешности для каждой из команд усреднены.
Среднее значение погрешностей определяется как САО (то есть, среднее абсолютное отклонение). В данном случае погрешность для каждой из команд составляет около 2%.
Для прогнозирования этого процента также можно использовать еще одну формулу:
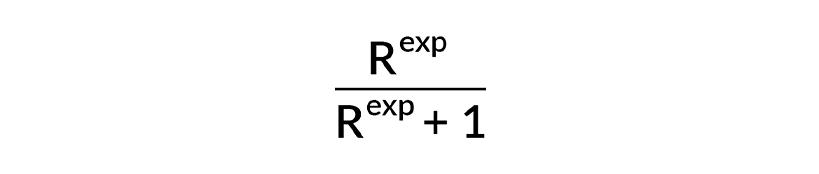
В данной формуле exp – это показатель степени. Изменяя его, возможно достичь более точного аппроксимирования реальной зависимости процента побед команды от показателя набора очков для некоторых видов спорта. Приемлемый показатель степени для бейсбола равен от 1 до 3, а если он равен 2, формула превращается в теорему Пифагора.
На этом графике вы увидите, как изменяется САО при колебании показателя степени от 1,1 до 3.
| exp | САО |
exp |
САО |
|
1,1 |
0,0297 | 2,1 | 0,0200 |
| 1,2 | 0,0277 | 2,2 | 0,0207 |
| 1,3 | 0,0259 | 2,3 | 0,0216 |
| 1,4 | 0,0243 | 2,4 | 0,0228 |
| 1,5 | 0,0228 | 2,5 | 0,0243 |
| 1,6 | 0,0216 | 2,6 | 0,0260 |
| 1,7 | 0,0206 | 2,7 | 0,0278 |
| 1,8 | 0,0200 | 2,8 | 0,0298 |
| 1,9 | 0,0196 | 2,9 | 0,0318 |
| 2,0 | 0,0197 | 3,0 | 0,0339 |
Наименьшее САО мы получим при exp = 1,96. При exp = 2 САО увеличивается всего на 0,01%, поэтому мы определяем, что именно значение exp = 2 является оптимальным.
Разумеется, возможно существование более точного уравнения, которое прогнозирует процент побед лучше, чем теорема Пифагора. Однако она не является сложной, доступна для понимания, и с ее помощью можно получить отличный результат. Это избавляет игроков от необходимости поисков более точной модели.


Все о ставках на бейсбол для профессионалов: проверка точности на ретроспективных данных
Для проверки любой модели прогнозирования, в том числе и проверки корректности бейсбольной теоремы прогнозирования, нужно определить точность, с которой модель прогнозирует будущее. Для этого сравним прогноз теоремы Пифагора для каждой серии игр МЛБ с выбыванием (1980 – 2007) и прогноз, построенный исключительно на победных играх. Получаем следующие данные:
- Для серии игр с выбыванием теорема Пифагора прогнозирует победу в серии той команды, которая имеет более высокий показатель набора очков. Данный метод прогноза является правильным в 57 из 106 сериях игр с выбыванием (53,8%).
- Подход на основе числа побед прогнозирует, что победителем серии игр с выбыванием будет команда, которая победила в большем количестве игр. Этот подход правильно прогнозирует победителя только в 50% (50 из 100) серий игр с выбыванием.
- Дело в том, что 3,8% – это большое преимущество над традиционной моделью.
- Регулярный сезон – довольно малозначимый прогностический фактор для игр с выбыванием в бейсболе. Статистика регулярного сезона команды сильно зависит от показателей пяти стартовых питчеров, а во время игр с выбыванием команды задействуют лишь трех или четырех из них. Именно поэтому значительная часть данных регулярного сезона (игры с участием четвертого и пятого стартовых питчеров) не является существенной для прогнозирования результатов игр с выбыванием.
Рассмотрим еще один пример из того же сезона, демонстрирующий, что теорема Пифагора прогнозирует последующие показатели команды лучше, чем статистика побед и поражений команды. В качестве примера мы рассмотрим историю Washington Nationals в сезоне 2005. 4 июля 2005 года Washington Nationals занимала первое место со статистикой 50-32. Метод, основанный на количестве побед, прогнозировал итоговый статистический результат 99-63, а теорема Пифагора спрогнозировала итоговую статистику 80-82. В реальности команда Washington Nationals финишировала со статистикой 81-81.
Анализ ставок на бейсбол. Влияние переходов игроков
Еще одним плюсом теоремы Пифагора для ставок на спорт является тот факт, что с ее помощью можно проанализировать, как переход того или иного игрока влияет на количество дополнительных побед или поражений команды.
К примеру, команда на протяжении сезона набрала 850 очков, а потеряла 800. Затем команда поменяла игрока Джо, заработавшего 150 очков, на Грега. Грег принес команде уже 170 очков. Подобная замена добавит команде еще 20 очков. У команды с Джо в составе показатель R был равен 850 / 800 = 1,0625, то есть, с данным игроком в составе команда должна была одержать победу в 162*(1,0625)2 / (1 + (1,0625)2) = 85,9 играх.
Показатель команды с Грегом в составе изменился, теперь R составляет 870 / 800 = 1,0875. Соответственно, команда одержит победу в 162*(1,0875)2 / (1 + (1,0875)2) = 87,8 играх. Исходя из этих данных можно предположить, что замена Джо на Грега сделает команду в 87,8 - 85,9 = 1,9 игр успешнее. Данную информацию о пользе, которую приносит команде тот или иной игрок, можно успешно использовать для построения стратегии ставок на бейсбол.
Саберметрика, как и математика бейсбола в целом, представляет собой огромный пласт для беттинга. Бетторы могут строить собственные модели ставок на бейсбол, основываясь на множестве уже готовых исследований, цифр и расчетов. Использование саберметрического анализа помогает бетторам получить преимущество над пулом игроков.
Чтобы не пропустить выход новых материалов, обязательно подписывайтесь на нас в соцсетях (Telegram, VK, Facebook) и на наш канал в YouTube.


















